Hệ Thống Kiến Thức Và Các Dạng Toán Lớp 4

Lớp 1

Lớp 2

Lớp 2 - liên kết tri thức

Lớp 2 - Chân trời sáng sủa tạo

Lớp 2 - Cánh diều

Tài liệu tham khảo

Lớp 3

Sách giáo khoa

Tài liệu tham khảo

Sách VNEN

Lớp 4

Sách giáo khoa

Sách/Vở bài tập

Đề thi

Lớp 5

Sách giáo khoa

Sách/Vở bài bác tập

Đề thi

Lớp 6

Lớp 6 - kết nối tri thức

Lớp 6 - Chân trời sáng sủa tạo

Lớp 6 - Cánh diều

Sách/Vở bài tập

Đề thi

Chuyên đề và Trắc nghiệm

Lớp 7

Sách giáo khoa

Sách/Vở bài xích tập

Đề thi

Chuyên đề và Trắc nghiệm

Lớp 8

Sách giáo khoa

Sách/Vở bài tập

Đề thi

Chuyên đề & Trắc nghiệm

Lớp 9

Sách giáo khoa

Sách/Vở bài tập

Đề thi

Chuyên đề và Trắc nghiệm

Lớp 10

Sách giáo khoa

Sách/Vở bài xích tập

Đề thi

Chuyên đề và Trắc nghiệm

Lớp 11

Sách giáo khoa

Sách/Vở bài tập

Đề thi

Chuyên đề & Trắc nghiệm

Lớp 12

Sách giáo khoa

Sách/Vở bài xích tập

Đề thi

Chuyên đề & Trắc nghiệm

Ngữ pháp tiếng Anh

Lập trình Java

Phát triển web

Lập trình C, C++, Python

Cơ sở dữ liệu

Công thức, Định nghĩa Toán, Lí, HóaĐường thẳngHình tam giácCác trường vừa lòng tam giác bởi nhauHình thangHình bình hànhHình thoiHình chữ nhật

Tổng hợp kỹ năng và kiến thức cơ bản Toán lớp 4 học tập kì 1, học tập kì 2 bỏ ra tiết

Tải xuống

SỐ TỰ NHIÊN

1. Số với chữ số

- dùng 10 chữ số nhằm viết số là: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

● tất cả 10 số có một chữ số (từ 0 mang đến 9)

● có 90 số có 2 chữ số (từ 10 cho 99)

● tất cả 900 số có 3 chữ số (từ 100 mang đến 999)

● tất cả 9000 số có 4 chữ số (từ 1000 mang lại 9999)

- Số trường đoản cú nhiên nhỏ nhất là số 0. Không tồn tại số tự nhiên lớn nhất.

Bạn đang xem: Hệ thống kiến thức và các dạng toán lớp 4

- nhì số tự nhiên thường xuyên hơn (kém) nhau một đối kháng vị.

- các số bao gồm chữ số tận thuộc là 0, 2, 4, 6, 8 call là số chẵn. Nhì số chẵn thường xuyên hơn hèn nhau 2 solo vị.

- những số bao gồm chữ số tận cùng là 1, 3, 5, 7, 9 hotline là số lẻ. Hai số lẻ thường xuyên hơn nhát nhau 2 đối chọi vị.

2. Hàng cùng lớp

* Lớp nghìn

Số	Lớp nghìn	Lớp 1-1 vị
Trăm nghìn	Chục nghìn	Nghìn	Trăm	Chục	Đơn vị
567				5	6	7
34 567		3	4	5	6	7
234 567	2	3	4	5	6	7

Hàng 1-1 vị, sản phẩm chục, hàng trăm ngàn hợp thành lớp đơn vị.

Hàng nghìn, hàng chục nghìn, hàng trăm ngàn hợp thành lớp nghìn.

3. Triệu cùng lớp triệu

Số	Lớp triệu	Lớp nghìn	Lớp đơn vị
Trăm triệu	Chục triệu	Triệu	Trăm nghìn	Chục nghìn	Nghìn	Trăm	Chục	Đơn vị
123 456 789	1	2	3	4	5	6	7	8	9

BIỂU THỨC

A. Các loại biểu thức thường gặp

1. Biểu thức có chứa một chữ

Ví dụ: 3 + a là biểu thức bao gồm chứa một chữ

+ giả dụ a = 1 thì 3 + a = 3 + 1 = 4; 4 là quý giá của biểu thức 3 + a

+ ví như a = 2 thì 3 + a = 3 + 2 = 5; 5 là quý hiếm của biểu thức 3 + a

+ nếu như a = 3 thì 3 + a = 3 + 3 = 6; 6 là cực hiếm của biểu thức 3 + a

2. Biểu thức bao gồm chứa hai chữ

Ví dụ: a + b là biểu thức bao gồm chứa hai chữ

+ trường hợp a = 3 và b = 2 thì a + b = 3 + 2 = 5; 5 là quý hiếm của biểu thức a + b

+ trường hợp a = 4 và b = 0 thì a + b = 4 + 0 = 4; 4 là giá trị của biểu thức a + b

+ ví như a = 0 và b = 1 thì a + b = 0 + 1 = 1; 1 là giá trị của biểu thức a + b

Mỗi lần cố chữ số thông qua số ta tính được một quý hiếm của biểu thức a + b.

3. Biểu thức gồm chứa tía chữ

Ví dụ: a + b + c là biểu thức gồm chứa ba chữ

+ giả dụ a = 2, b = 3 với c = 4 thì a + b + c = 2 + 3 + 4 = 5 + 4 = 9

+ nếu như a = 5, b = 1 với c = 0 thì a + b + c = 5 + 1 + 0 = 6 + 0 = 6

+ nếu a = 1, b = 0 và c = 2 thì a + b + c = 1 + 0 + 2 = 1 + 2 = 3

B. Cách tính giá trị của biểu thức

1. Biểu thức không có dấu ngoặc 1-1 chỉ tất cả phép cùng và phép trừ (hoặc chỉ tất cả phép nhân và phép chia) thì ta thực hiện các phép tính theo vật dụng tự từ trái sang phải.

Ví dụ:

a) 542 + 123 – 79 = 665 – 79 = 586

b) 482 × 2 : 4 = 964 : 4 = 241

2. Biểu thức không tồn tại dấu ngoặc đơn, có những phép tính cộng, trừ, nhân, phân chia thì ta tiến hành các phép tính nhân, phân chia trước rồi thực hiện các phép tính cùng trừ sau.

Ví dụ: 27 : 3 - 4 × 2 = 9 - 8 = 1

3. Biểu thức bao gồm dấu ngoặc đối kháng thì ta thực hiện các phép tính trong ngoặc 1-1 trước, các phép tính bên cạnh dấu ngoặc đơn sau.

Ví dụ: 25 × (21 + 120) = 25 × 141 = 3525

BỐN PHÉP TÍNH VỚI SỐ TỰ NHIÊN

A. PHÉP CỘNG

1. đặc điểm giao hoán

a + b = b + a

Ví dụ: 2 + 3 = 3 + 2

2. Tính chất phối kết hợp của phép cộng

(a + b) + c = a + (b + c)

Ví dụ: (2 + 3) + 4 = 2 + (3 + 4)

3. Cùng với 0

0 + a = a + 0 = a

Ví dụ: 0 + 9 = 9 + 0

Nhận xét:

+ vào một tổng có số lượng các số hạng lẻ là lẻ thì tổng kia là một vài lẻ.

+ trong một tổng có con số các số hạng lẻ là chẵn thì tổng kia là một số chẵn.

+ Tổng của những số chẵn là một số trong những chẵn.

+ Tổng của một vài lẻ và một vài chẵn là một trong những lẻ.

+ Tổng của nhì số từ nhiên liên tiếp là một trong những lẻ.

B. PHÉP TRỪ

1. a - (b + c) = (a - c) - b = (a - b) - c

2. Nếu số bị trừ cùng số trừ cùng tăng (hoặc giảm) n đơn vị chức năng thì hiệu của chúng không đổi.

3. Nếu số bị trừ được vội lên n lần và giữ nguyên số trừ thì hiệu được tăng thêm một số trong những đúng bằng (n - 1) lần số bị trừ (n > 1).

4. Nếu số bị trừ giữ nguyên, số trừ được vội lên n lần thì hiệu bị sụt giảm (n - 1) lần số trừ (n > 1).

5. Nếu số bị trừ được tăng thêm n solo vị, số trừ giữ nguyên thì hiệu tăng thêm n đối kháng vị.

6. Nếu số bị trừ tăng thêm n đơn vị, số trừ giữ nguyên thì hiệu giảm xuống n đối kháng vị.

C. PHÉP NHÂN

1. Tính hóa học giao hoán

a × b = b × a

Ví dụ: 2 × 3 = 3 × 2

2. Tính hóa học kết hợp

a × (b × c) = (a × b) × c

Ví dụ: 2 × (3 × 4) = (2 × 3) × 4

3. Nhân với 0

a × 0 = 0 × a = 0

Ví dụ: 2 × 0 = 0 × 2 = 0

4. Nhân cùng với 1

a × 1 = 1 × a = a

Ví dụ: 4 × 1 = 1 × 4 = 4

5. Tính chất cung cấp của phép nhân với phép cộng

a × (b + c) = a × b + a × c

Ví dụ: 3 × (2 + 3) = 3 × 2 + 3 × 3

6. tính chất phân phối của phép nhân với phép trừ

a × (b - c) = a × b - a × c

Ví dụ: 6 × (9 – 3) = 6 × 9 – 6 × 3

7. trong một tích nếu một vượt số được vội lên n lần đồng thời có một thừa số không giống bị giảm đi n lần thì tích không cầm cố đổi.

8. trong một tích tất cả một thừa số được vội lên n lần, các thừa số còn lại không thay đổi thì tích được gấp lên n lần và trái lại nếu vào một tích tất cả một thừa số bị giảm sút n lần, các thừa số còn lại không thay đổi thì tích cũng trở thành giảm đi n lần. (n > 0)

9. Trong một tích, nếu như một thừa số được cấp lên n lần, đồng thời một thừa số được vội lên m lần thì tích được vội lên (m × n) lần. Ngược lại nếu trong một tích một vượt số bị giảm sút m lần, một thừa số bị giảm đi n lần thì tích bị giảm xuống (m × n) lần (m cùng n khác 0).

10. Vào một tích, ví như một quá số được tăng lên a đơn vị, những thừa số còn lại giữ nguyên thì tích được tạo thêm a lần tích những thừa số còn lại.

11.

Xem thêm: Vải Áo Dài Màu Hoa Mười Giờ Thủy Chung Mẫu L17059, Hoa Mười Giờ

vào một tích, nếu như có tối thiểu một quá số chẵn thì tích đó chẵn.

12. Trong một tích, ví như có tối thiểu một vượt số tròn chục hoặc ít nhất một thừa số bao gồm tận cùng là 5 cùng có ít nhất một vượt số chẵn thì tích có tận cùng là 0.

13. Trong một tích những thừa số các lẻ và có tối thiểu một vượt số bao gồm tận thuộc là 5 thì tích gồm tận cùng là 5.

D. PHÉP CHIA

1. a : (b × c) = a : b : c = a : c : b (b, c > 0)

2. 0 : a = 0 (a > 0)

3. a : c - b : c = ( a - b) : c (c > 0)

4. a : c + b : c = (a + b) : c (c > 0)

5. Trong phép chia, nếu như số bị chia tăng lên (giảm đi) n lần (n > 0) đôi khi số chia không thay đổi thì yêu mến cũng tăng thêm (giảm đi) n lần.

6. Trong một phép chia, nếu tăng số chia lên n lần (n > 0) bên cạnh đó số bị chia giữ nguyên thì thương sụt giảm n lần và ngược lại.

7. trong một phép chia, trường hợp cả số bị phân tách và số chia các cùng gấp (giảm) n lần (n > 0) thì mến không núm đổi.

8. trong một phép chia tất cả dư, ví như số bị chia và số chia cùng được cấp (giảm) n lần (n > 0) thì số dư cũng rất được gấp (giảm) n lần.

DÃY SỐ

1. Đối cùng với số tự nhiên và thoải mái liên tiếp

a) dãy số tự nhiên và thoải mái liên tiếp ban đầu là số chẵn xong là số lẻ hoặc bước đầu là số lẻ và chấm dứt bằng số chẵn thì số lượng số chẵn bằng con số số lẻ.

b) dãy số thoải mái và tự nhiên liên tiếp ban đầu bằng số chẵn và hoàn thành bằng số chẵn thì số lượng số chẵn nhiều hơn nữa số lượng số lẻ là 1.

c) hàng số tự nhiên liên tiếp bước đầu bằng số lẻ và chấm dứt bằng số lẻ thì con số số lẻ nhiều hơn nữa số lượng số chẵn là 1.

2. Một số trong những quy phép tắc của hàng số thường xuyên gặp

a) từng số hạng (kể tự số hạng sản phẩm 2) thông qua số hạng đứng tức tốc trước nó cùng hoặc trừ một vài tự nhiên.

Ví dụ: 2, 5, 8, 11, …

Dãy số trên được viết theo quy luật: Số hạng đứng ngay thức thì sau thông qua số hạng đứng ngay tức khắc trước cộng với 3.

b) mỗi số hạng (kể từ bỏ số hạng sản phẩm công nghệ 2) thông qua số hạng đứng tức khắc trước nó nhân hoặc chia một số tự nhiên.

Ví dụ: 1024, 512, 256, 128, …

Dãy số trên được viết theo quy luật: Số hạng đứng liền sau ngay số hạng đứng liền trước phân tách cho 2.

c) mỗi số hạng (kể tự số hạng sản phẩm 3) bằng tổng nhị số hạng đứng liền trước nó.

Ví dụ: 1, 2, 3, 5, 8, 13, 21,…

Dãy số được viết theo quy luật: tự số hạng trang bị ba, số hạng đứng sau bằng tổng nhì số hạng đứng liền trước nó (3 = 2 + 1, 5 = 3 + 2, 8 = 5 + 3, ….)

3. Hàng số bí quyết đều

*) tìm kiếm số số hạng của dãy số bí quyết đều

Số số hạng = (Số cuối – Số đầu) : khoảng cách giữa nhị số hạng tiếp tục + 1

Ví dụ. search số số hạng của dãy số: 1, 4, 7, 10, 13, 16, 19, …, 94, 97, 100

Bài giải

Số số hạng của dãy số đã mang lại là:

(100 – 1) : 3 + 1 = 34 (số hạng)

Đáp số: 34 số hạng

*) Tính tổng của dãy số bí quyết đều

Tổng = (Số đầu + Số cuối) × Số số hạng : 2

Ví dụ. Tính tổng của dãy số: 1, 4, 7, 10, 13, 16, 19, …, 94, 97, 100

Bài giải

Số số hạng của hàng số trên là: 34 số hạng

Tổng của hàng số trên là:

(100 + 1) × 34 : 2 = 1717

Đáp số: 1717

DẤU HIỆU phân chia HẾT

1. Tín hiệu chia hết mang đến 2

Các số gồm chữ số tận cùng là 0, 2, 4, 6, 8 thì phân chia hết đến 2.

Ví dụ:

12, 14, 16, 18 là các số chia hết cho 2 vì gồm chữ số tận thuộc là 2, 4, 6, 8

11, 13, 15, 17 là phần đông số không phân chia hết đến 2 vì có chữ số tận cùng là 1, 3, 5, 7

- Số phân tách hết cho 2 là số chẵn.

- Số không chia hết cho 2 là số lẻ.

2. Dấu hiệu chia hết cho 5

Các số gồm chữ số tận thuộc là 0 hoặc 5 thì phân chia hết cho 5.

Ví dụ:

945, 3000 là các số chia hết mang đến 5 do số đó tất cả chữ số tận thuộc lần lượt là 5, 0

10, 25 là phần lớn số phân tách hết mang lại 5 vày những số đó gồm tận thuộc là 0, 5

3. Tín hiệu chia hết đến 9

Các số bao gồm tổng những chữ số phân tách hết mang lại 9 thì chia hết đến 9.

Các số có tổng những chữ số không phân chia hết mang đến 9 thì không phân tách hết cho 9.

Ví dụ:

a) 657 : 9 = 73

Ta có:

6 + 5 + 7 = 18

18 : 9 = 2

b) 451 : 9 = 50 (dư 1)

Ta có:

4 + 5 + 1 = 10

10 : 9 = 1 (dư 1)

4. Dấu hiệu chia hết cho 3

Các số bao gồm tổng các chữ số phân tách hết mang đến 3 thì phân chia hết cho 3.

Các số có tổng những chữ số không phân tách hết mang lại 3 thì không phân tách hết đến 3.

Ví dụ:

a) 63 : 3 = 21

Ta có:

6 + 3 = 9

9 : 3 = 3

b) 125 : 3 = 41 (dư 2)

Ta có:

1 + 2 + 5 = 8

8 : 3 = 2 (dư 2)

CẤU TẠO SỐ

Sử dụng cấu trúc số:

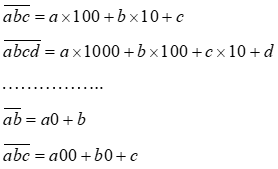
Ví dụ: mang đến số gồm 2 chữ số, nếu mang tổng các chữ số cộng với tích những chữ số của số đã mang đến thì bằng chính số đó. Tra cứu chữ số hàng đơn vị chức năng của số đang cho.